制订体质评定和科学选材标准的统计方法
(总结篇一)
【说明】 1979-1980年我国首次在16省、市开展青少年儿童体质研究,1985年国家教委、国家体委、卫生部联合对全国29省、市大、中、小学生开展体质、健康调查。从1980年国家体委组织委管课题“优秀青少年运动员选材研究”以来,运动员科学选材在全国各省、市也逐渐推广普及。制订评分、评价标准是体质研究和运动员科学选材研究中十分重要的研究内容。统计方法是研究评分、评价必须的工具,同时,在研究和制订标准的过程中,统计方法的应用也得到了丰富和发展。 本人从1979年参加全国青少年儿童体质研究起,一直从事体质评价的研究,1988年担任全国运动员科学选材中心组组长后,又协助国家体育总局科教司领导全国的科学选材标准研究工作。对制订评价标准的不同阶段,应该采用什么统计方法,逐渐积累了一些经验。1997年与原国家体育总局科教司领导高大安同志交谈,他认为很有必要将十多年来积累的经验加以总结,我就写了“制订科学选材标准的统计方法”,并被1997年11月在北京召开的第五届全国体育科学大会录取专题报告。
2000年以后,我在深圳、安徽、甘肃、深圳、河北、湖北等省市多次讲课或指导他们制订体质测定标准、运动员选材标准。这次进一步总结了2003-2017年讲课和研究工作的经验后,写成了这篇文章。 王路德 2020.2.22 一、历史的回顾 70年代末我国体质研究和运动员科学选材研究刚起步时,制订评分、评价标准只是沿用当时体育统计教材和卫生统计中的一些常用方法。如:用离差法(平均数加减标准差)、百分位数法制订评分标准,对多项指标的综合评价还没有“权”。 1984年全国体质研究学术报告会时,“对综合评价方法的研究有了较明显的进展”(见会议小结),会上多篇论文提出了不少统计方法如:逐步回归、判别分析、聚类分析等。会后,国家体委决定进一步集中力量组织综合评价方法的研究,于1985年成立了《中国学生体质综合评价方法研究》课题协作组,课题被列入国家体委委管课题。这是一个主要运用统计方法的研究课题,中国体育科学学会体育统计专业委员会的王路德,戎家增被邀加入课题组,王路德主要负责部分数据计算及指标标“权”的研究。课题组还邀请我国知名的概率统计专家张尧庭教授对“权”的研究作了专题指导。 1988年国家体委成立运动员科学选材中心组,我被聘为组长后,制订各运动项目科学选材标准及综合评价方法是主要工作任务之一。1989、1990年中心组两次召集有关省、市选材研究人员开会,专题讨论了制订选材标准时统计方法的运用问题,为1990-1992年中心组领导的国家体委课题(九个运动项目科学选材标准研究)作了统计方法的准备。 2000年以后我在指导深圳、安徽、甘肃、河北、陕西、山西、湖北等省市体育科研所、体质监测中心制定或修改选材或体质标准时,在参加体质研究和运动员科学选材研究的委管课科研人员共同努力下,不仅完成了研究任务,而且对统计方法在评分、评价中的应用也作了许多探索。十分有必要加以总结。
二、 制订“标准”的四个阶段 无论是制订体质评价标准还是制订运动员选材标准,整个研究过程中都应分为四个阶段,即:筛选指标、制订单项指标的评分标准、确定各指标的权重系数和综合评价方法、标准(初稿)试用验证后的修改。每一研究阶段都要采用不同的统计方法。 1.筛选指标 为了从大量可用的指标中选定最关键的指标,必须进行指标筛选。通常可用两种方法: 1.1 特尔斐法(专家调查法) 首先通过文献资料收集,整理出准备选用的指标(选用时要注意指标的可靠性、有效性、客观性)。把初步整理出的指标印成调查问卷表,发给对本项目有经验的专家,征求他们的意见。对回收的调查表作统计处理,主要可通过作频数分布表,计算平均数、众数等,从而找出专家们意见比较集中的指标。按照特尔斐法的要求,应把第一轮意见的统计结果再次印发给专家,征求他们的意见。这样经过两轮咨询,一般都能取得较一致的意见。但在研究工作中我们发现,第二轮意见印发后,如果能请专家们来开一次咨询座谈会效果会更好。 1.2 数据统计法 可以用多因素统计方法中的逐步回归、R型聚类等,通过计算筛选出其中较重要的指标。如:1987年我在作赛艇选材标准研究时,用R型聚类分析计算出选材指标谱系图如图1, 由图可见,当将指标分成七类时有‘*’的为每类的典型指标。该项计算结果成为后来确定赛艇选材标准中的形态、机能类指标的主要依据。 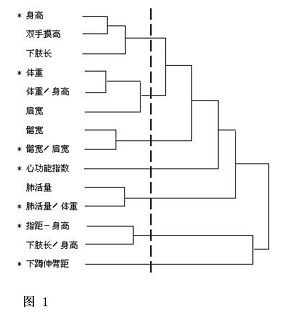
1987年全国选材协作组曾对我国大批优秀田径运动员的数据做过逐步回归计算,发给有关省市。计算时,以运动成绩为因变量Y,自变量Xi是形态、机能、素质指标。其中样本量较大的项目,计算结果对筛选指标很有参考价值。 但是,用逐步回归计算时,必须特别注意样本量 n 和指标数 k的比例,如 n 太小计算的结果就不能用。因为,多元回归方程的系数bi 的解是和原始数据的组数(样本含量)n 紧密相关的,可以推导出:当 n=k+1时,即使k个自变量Xi和Y全都不相关,仍可计算出复相关系数R=1的多元回归方程。所以,n 最好达到k 的5-10倍。 研究工作的实践表明:有时单靠统计计算结果来确定选材指标是不行的。因为指标筛选需要考虑的因素很多,如:指标的信度、效度、运动项目自身的特点等,这些因素在计算结果中有些能得到体现,而有些则难以体现。为了避免单纯依据计算结果而导致的指标体系建立的偏差。较好的办法是:在统计计算和“特尔斐”法调查的基础上,再组织有经验的专家座谈讨论,经过全面慎重的考虑,最后确定指标。 2. 制订单项指标的评分标准 每一个单项指标,如:身高、体重、肺活量……等,都应该分别制订出评分标准。一个单项指标的评分标准应该分为几个等级,各等级应如何划分? 这些在体育统计学里并无现成的规定,要由标准制订者研究确定。 1980年“中国青少年儿童体质研究”中,形态、机能指标都是分为:上、中上、中、中下、下五等,素质指标设1-20分,2003年国民体质测定标准分5等。1980年“优秀青少年运动员选材研究”中,田径分上、中、下三等,足球分五等…… [3]。1987年以后,各省市制订的标准有的分三等、有的分五等、也有分十等的。 1985年《中国学生体质综合评价方法与标准》规定各单项指标均按公式计算标准分,公式为:  
为了使用方便,事先按公式计算出各指标的评分表,使用时直接根据测试值查出单项指标的得分。但是,这种方法计算出的评分表篇幅太大。按公式用手工计算则比较麻烦。 1989年全国选材中心组扩大会讨论认为,通过评分只需表明受测者的某指标值(如:身高170.5厘米)按某运动项目的要求,可划入优、良、中、差的哪一范围,不必分得太细。而且评分等级分得过细制订出的评分表必然很繁琐,使用较不方便。所以,评分标准“宜粗不宜细”。因此,1990年制订全国统一的九个项目选材标准和1992年制订八个项目选材标准时,以及后来好多省制订选材标准时都是分为5等。并规定用平均数加减标准差的方法划分等级,如表1。但是,有一些指标并不是测试值越大越好或越小越好,而是中间值好,太大或太小都不好。例如:指标身高,在篮球、排球选材时是测试值越大越好,而在体操、跳水选材中的身高指标都是太大或太小都不好,而在中间范围内最好。还有如评定身体结实程度的克托莱指数,BMI指数等指标也是这样。所以,分5个等级时,就不是1、2、3、4、5等,而是1、3、5、3、1了,如表2。 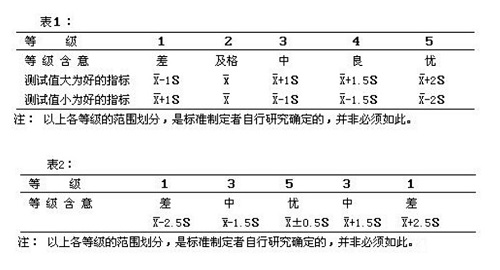
2003年修改公布的《国民体质测定标准》,制订标准时规定,各单项指标的评定也是分为5个等级,用百分位数制订,划分的界限和各等级内理论分布人数的百分比见表3。
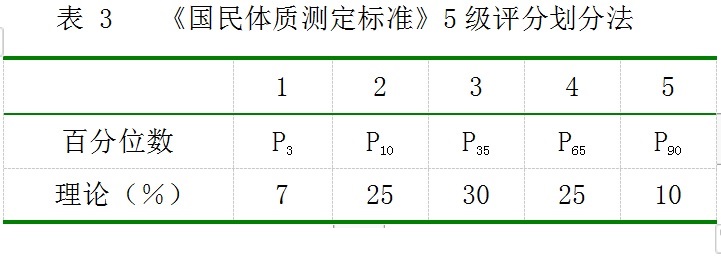
2.1 标准的年龄段划分
制订不同年龄段的评定标准时,要根据人体生长发育的不同阶段来确定评分标准的年龄划分方法。运动员选材标准都是一岁一个年龄组。国家国民体质监测中心在研制我国《国民体质测定标准》时,考虑到不同年龄人群在体质方面的不同特征和差异,规定了分组制订标准的年龄段划分方法,见表4。

由2000年起每5年一次的国民体质监测公布的统计数据可见,7岁到18岁间青少年各项测试指标平均数都呈现不断增长的趋势。尤其是进入青春发育期后,许多指标都出现突增期,表现为:年增长值很大。因此,对青少年学生的体质评定必须以年龄为单位来制订标准,才能看出每个学生身体的形态、机能、素质的各项指标在同年龄人中处于什么水平。
但是,2003年公布的《学生体质健康标准》却是按学生的上课班级制订标准,即一个年级1个标准,我们认为这是很不合适的。因为在同一个年级至少会有3个不同年龄的学生。我们于2007年调查了某市13所中学55个班的2136名初三学生,其中15岁占59.18%,14岁占20.2%,16岁的占14%,甚至最小的是11岁,最大的是20岁。此统计数据充分说明了在一个年级里,学生的年龄差别很大,用相同的标准对他们进行体质评定是极不合理的。 2.2 不同年龄段的评定标准要特别注意与该指标的发育趋势一致。 制订各年龄段的标准,不能简单地用测试到的样本,按离差法或百分位数法制订各等级的标准。还必须纵向查看,查看各年龄标准的年增长值是否与该指标的发育趋势一致。 如1990年制订全国的选材标准《运动员科学选材》时,虽然强调了要用优秀运动员的模式数据为依据,推算制订各个年龄的选材标准,但是,标准中还是有一些不尽合理的地方。以田径男短跑的身高标准为例,其17岁等级2(合格)的标准大体与全国身高平均数相同,但是,15岁的标准明显低于全国身高平均数,而12岁则大大高于全国平均数。由表5和图2可以看得出:无论等级2(合格)还是等级5(优秀)随年龄而增加的标准,与正常青少年的身高生长发育曲线是很不一致的。因此,这就造成了各年龄段选材标准的难易度不一致。 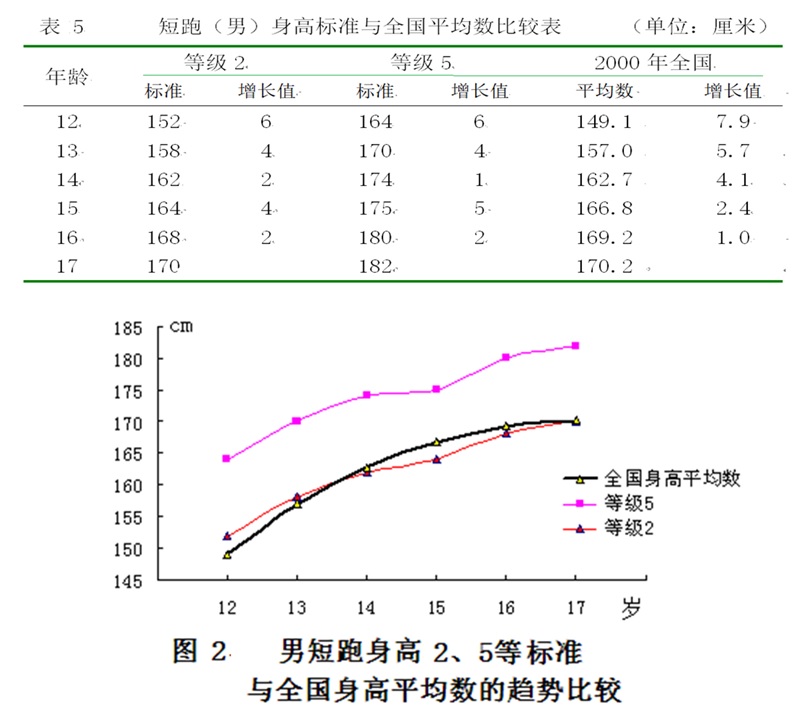
产生以上问题的原因,是当年在制订各指标标准时,没有特别强调:要检查随年龄增大而变化的不同年龄段标准,是否与该指标青少年时期的发育趋势一致。 2.3 用优秀运动员模式×定基比法,制订选材标准中各年龄组的标准。 由于制订选材标准的目的是要选拔未来的优秀选手,所以,各年龄组的标准都应该以优秀运动员的“模式”数据为依据。为此,首先要通过测试或收集文献资料,取得全国或世界的优秀成年运动员各指标的平均数、标准差,在此基础上规定出成年时各指标的“模式”等级要求,如:某项目成年男子运动员“模式”数据为身高175厘米为及格、190厘米为优秀等等。
再采用优秀运动员“模式”数据乘各年龄组定基比的方法制订各年龄组的标准,这样才能保证该指标年龄组间的增长值符合青少年的生长发育曲线规律。 我国从1979年以来的历次青少年,学生体质调查,和2000年起全国开展的大规模国民体质监测所获得的各指标测试数据,提供了许多指标的青少年发育规律。用某一指标各个年龄组的平均数就可以用统计方法计算出该指标的定基比。 定基比:是以某一时期(年龄)的数据为基准,把它定为100%,其他时期(年龄)的数据都和它比较,增长(或减少)的百分比。 以2000年全国国民体质监测公布的男身高平均数为例。计算定基比时,如果把18岁身高平均数170.2定为100%,则7岁身高平均数122.6是18岁身高平均数的0.72(122.6/170.2),12岁是18岁的0.876(149.1/170.2)……(见表6)。 假设通过测试或查阅文献资料,确定某项目18岁优秀运动员的身高“模式”数据,优秀为190厘米。则其他各年龄组身高的优秀标准,只要用190×定基比就可计算出来(见表6)。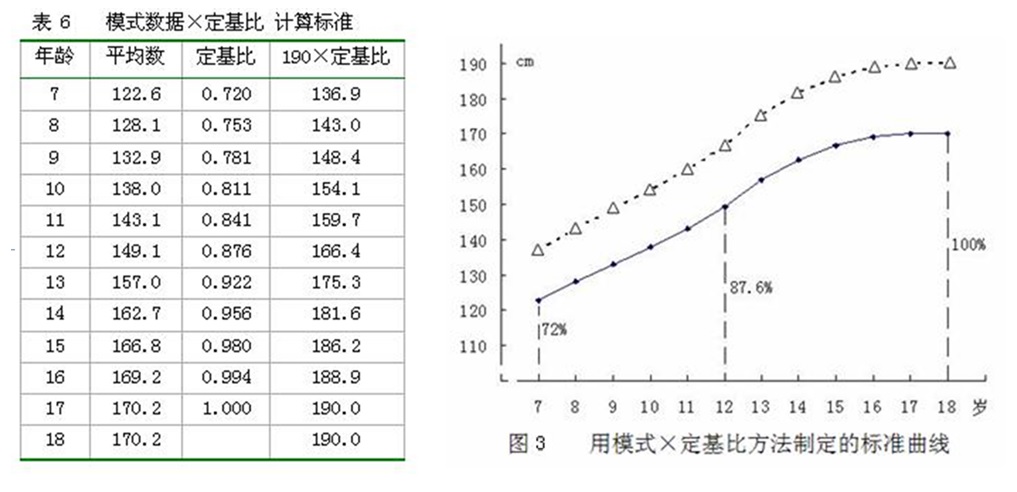 由图3可见,用模式数据×定基比计算出的各年龄段标准(虚线)与青少年身高的发育曲线(实线)趋势是完全一致的。 在运用定基比法制订标准时,我们曾遇到一个特例。选材中一项形态派生指标:“指距-身高”在 10岁前为负值(见图4),如果仍按体育统计中定基比的计算方法,则10岁前的定基比为负值(见表7),显然不对。解决的办法是先给各年龄组的平均数X 加一个常数C,把负值变换为正值后,再计算定基比(见表8)。 但是,C取多少合适呢?C值定得大小不同,会直接影响各年龄组和18岁组的比值,其差别会很大。我们是这祥解决的,根据已有的统计资料可知,指距随年龄而变化的趋势和身高是一致的,而且两者的平均数差距也不太大,身高的定基比己知,因此可以用身高的定基比来推算C值。如计算男指距-身高的C值时,根据男7岁的身高定基比为70%,则: ( -1.22 + C ) ────────── = 0.7 C = 13.21 3.92 + C 注:-1.22和3.92 为7,18岁的指距-身高平均数 而用定基比计算各年龄组标准时要改用下列公式: 年龄组标准=(X+C)×定基比-C [6] 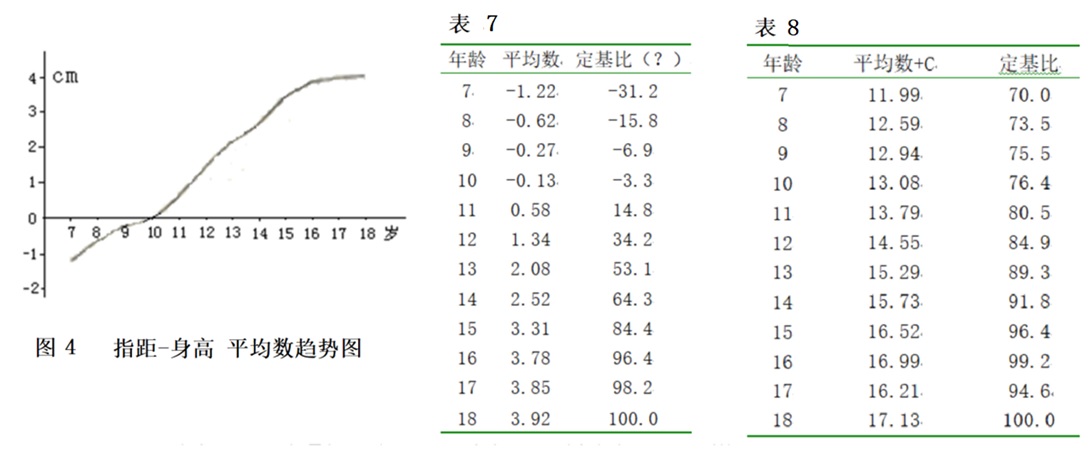
2.4 用离差法制订各年龄组标准后,必须作平滑处理。 凡是还没有定基比数据的指标,可采用离差法制订标准。为此需要先测试一批各年龄组该指标的 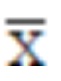 、S。但是,即使测试的样本量较大,也必然会由于抽样误差而使测得的 、S。但是,即使测试的样本量较大,也必然会由于抽样误差而使测得的 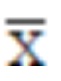 、S,存在年龄组间的起伏波动。如果直接用这些 、S,存在年龄组间的起伏波动。如果直接用这些 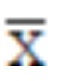 、S按离差法制订标准,由于平均数和标准差两者的随机波动影响叠加在一起,会使得标准起伏更大,相邻年龄组间很可能会出现许多不合理的地方。如某小年龄组的标准反而比大年龄组的高。因而,必须用曲线拟合法对测得的 、S按离差法制订标准,由于平均数和标准差两者的随机波动影响叠加在一起,会使得标准起伏更大,相邻年龄组间很可能会出现许多不合理的地方。如某小年龄组的标准反而比大年龄组的高。因而,必须用曲线拟合法对测得的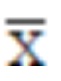 、S先作平滑处理后再按离差法制订出的标准才能使用。 、S先作平滑处理后再按离差法制订出的标准才能使用。 如:1991年在制订 7~17岁心功能指数标准时,虽然各年龄组测试的样本量均较大,但是计算出的 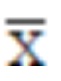 、S各年龄组之间仍然存在着随机波动,7~17岁的 、S各年龄组之间仍然存在着随机波动,7~17岁的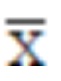 总的趋势是随年龄的增长而减小,但波动较大,S也存在着随机波动。因而我们先进行了平滑处理,对各年龄组的 总的趋势是随年龄的增长而减小,但波动较大,S也存在着随机波动。因而我们先进行了平滑处理,对各年龄组的 、S分别用直线、对数曲线、指数曲线、双曲线和抛物线进行拟合,图5是平均数的曲线图,计算结果表明抛物线的拟合优度最好,标准差曲线的拟合结果相同(图略)。最后,就用抛物线方程计算出平均数和标准差的平滑值,再用离差法制订各年龄组的标准,使用效果较好。 、S分别用直线、对数曲线、指数曲线、双曲线和抛物线进行拟合,图5是平均数的曲线图,计算结果表明抛物线的拟合优度最好,标准差曲线的拟合结果相同(图略)。最后,就用抛物线方程计算出平均数和标准差的平滑值,再用离差法制订各年龄组的标准,使用效果较好。 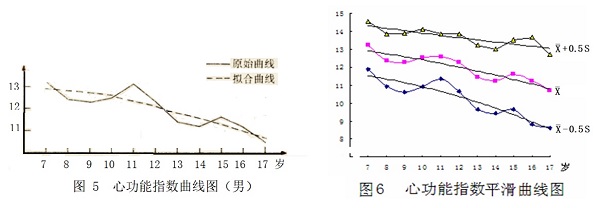
由图6可见,假设对每个年龄组用平滑后的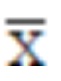 +0.5 S, +0.5 S, , ,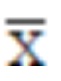 -0.5 S的方法制订3个标准时,平滑处理后的趋势明显的比未处理前合理。[6] -0.5 S的方法制订3个标准时,平滑处理后的趋势明显的比未处理前合理。[6]
有些指标,各年龄段的平均数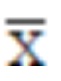 呈现上下起伏,即使作数据平滑处理后,仍然显示出并非逐年上升的趋势。如:下肢长A /身高×100的平均数就是从7岁起逐年加大,到13、14岁时达到最大,以后逐渐减小(见图7)。由于这一趋势是符合青少年青春发育期,先长四肢、后长躯干的“向心律”规律对下肢比例的影响的。因此,在制定各年龄组标准时就必须注意使标准符合这一客观规律。 呈现上下起伏,即使作数据平滑处理后,仍然显示出并非逐年上升的趋势。如:下肢长A /身高×100的平均数就是从7岁起逐年加大,到13、14岁时达到最大,以后逐渐减小(见图7)。由于这一趋势是符合青少年青春发育期,先长四肢、后长躯干的“向心律”规律对下肢比例的影响的。因此,在制定各年龄组标准时就必须注意使标准符合这一客观规律。 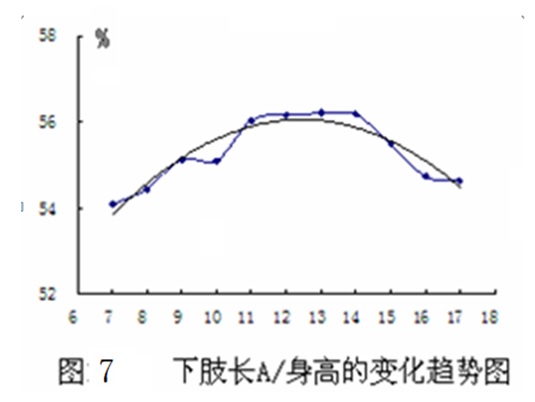
所以,在制订某指标的各年龄组标准时,千万不要没有依据,就把标准制定为随年龄增大而逐年提高,或把某几个年龄的标准定成相同。 2.5 用百分位数法制订各年龄组标准后,必须纵向查看,决定是否要平滑处理。 从1979年的“中国青少儿体质调查”到1995年的“中国学生体质与健康调研”每次都统计公布各单项指标各年龄、性别组的百分位数(P3、P5、P10、P15、P25、P30、P50、P70、P75、P85、P90、P95、P97)。各指标的百分位数可以是制订单项标准的依据。但是,用百分位数来制订各年龄组的单项标准时,从理论上说,也仍然会由于抽样误差而使计算出的标准在年龄组间有起伏波动。因此,如果发现计算出的标准在各年龄组间有不合理的起伏波动,还是应该作平滑处理。 以《体质测定标准》的幼儿男生网球掷远为例,虽然这是用大样本的国民体质监测数据按百分位数法制定出的标准。但是通过纵向查看增长值,仍可以发现不合理的地方。(见表9)。 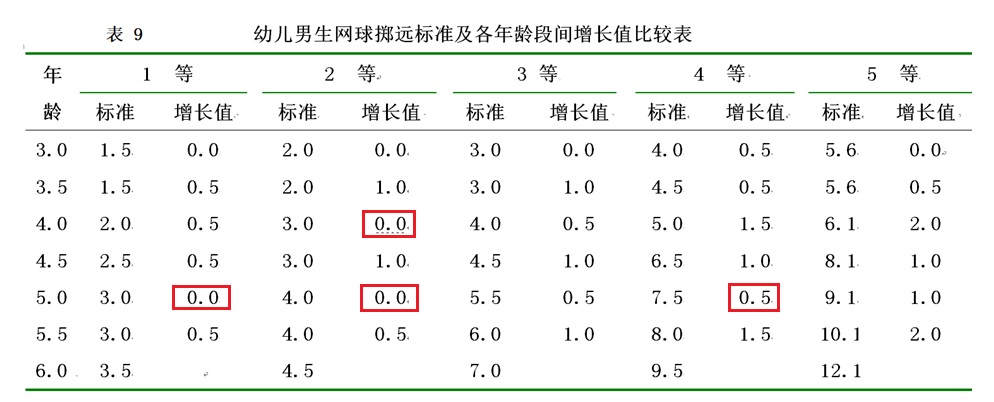
由表9可见,4.0岁2等标准为3.0米,而4.5岁2等标准也为3.0米,年龄段间增长值为0。但是,其他等级的增长值为0.5至2.0不等。如果说对4等、5等要求高一点,所以,增长值要加大一些,那么为什么2等的要求比1等还低呢?类似的现象在5岁和5.5岁之间也有。产生以上现象的原因,就是制定标准时,只注意了每个年龄内5个等级之间的合理性(如规定了划分的界限和各等级内理论分布人数的百分比),但是,没有对各年龄组之间,相同等级的标准进行纵向的增长值比较。 2.6 用回归分析法制订标准 有时某个指标的某些年龄段不能测到较大的样本,因此无法采用离差法或百分位数法制订标准。这时只能采用回归分析方法处理。 有一个实例:某省制订田径运动员选材标准时,有一项专项素质指标是立定三级跳远。但是,当时只测到45名11至18岁男田径运动员的立定三级跳远数据。其各年龄组人数分布如表10。由于受到许多客观因素的限制,一时无法再扩大样本,因此决定试用回归分析方法进行处理。
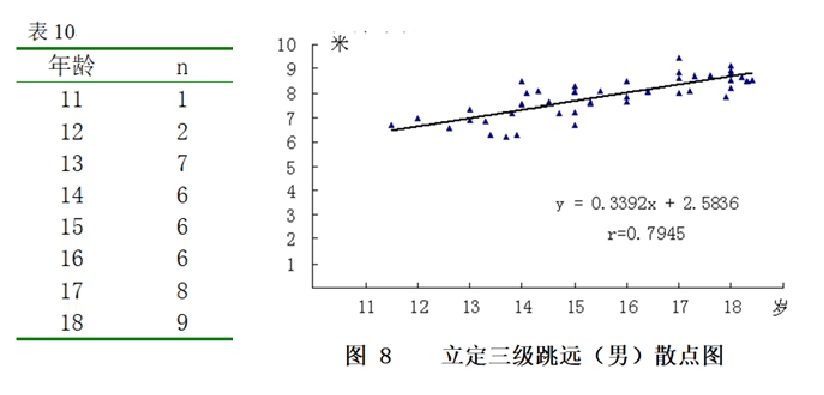
首先用原始数据做散点图,通过添加趋势线,看数据的变化趋势是否符合随年龄增长而变化的趋势,决定能否使用回归方程制定标准。如果趋势线不符合随年龄增长而变化的趋势,或者相关程度很差就不能用了。 本例作出的散点图(图8),图上用一元回归方法添加趋势线,并可计算出年龄和立定三级跳远的一元回归方程: Y=2.5836+0.3392 X 相关系数:r=0.7945(P<0.01) 由于从趋势线可以看出,立定三级跳远的成绩是随年龄增加而逐渐增加,符合青少年的发育特点。而且相关系数 r=0.7945,呈高度相关。因此,可以认为计算出的一元回归方程,反映了11至18岁男运动员的年龄和立定三级跳远成绩呈线性关系。决定用一元回归方程来制定各年龄组的标准。先用一元回归方程:Y=2.5836+0.3392 X 推算出各年龄的立定三级跳远回归值,把它作为各年龄组的第2等标准。 再用45人的立定三级跳远数据计算出标准差为:0.8271。 由正态分布表可查到,如果把平均数作为标准,约有50%的人可达到标准,平均数-0.25标准差则约有60%的人可达到标准,用平均数+0.25、+0.52、+0.84标准差制定标准约有40%、30%、20%的人可达到标准。本例用各年龄组回归值-0.25标准差、+0.25标准差、+0.52标准差、+0.84标准差可计算出1至5等标准,如图9。 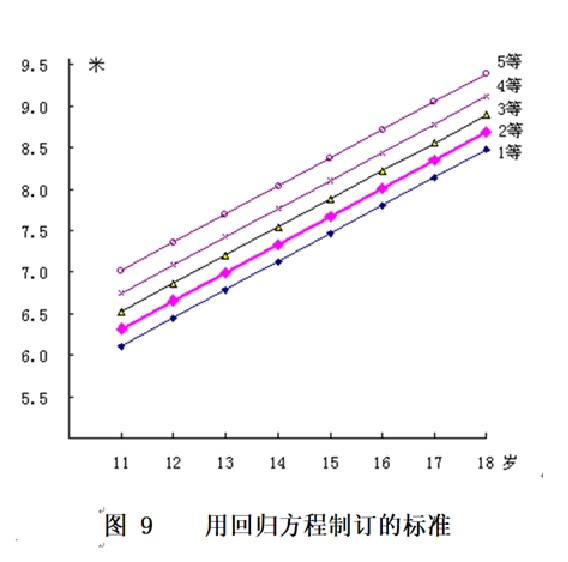
采用回归方程制订的标准,特别需要在小范围试用后,收集反馈的意见,再作必要的修改后定稿。
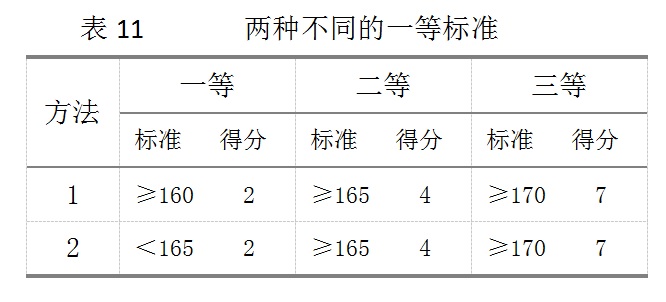
2.7 最低等级标准的两种订法 最低的一等标准可以有两种订法。下面以分三个等级的身高标准为例(见表11),由表11可见,方法1规定了达到一等的下限,凡是达不到下限160的,就得不到分。而方法2则是凡达不到二等的都评为一等,即至少可获得2分。这就要根据标准制订者对某项指标的要求来决定采用那种方法了。 方法1 的要求较严,达不到最低要求就没有分,素质类、机能类指标可采用。而方法2 则相对松一些,常在形态指标中用此方法。
本文后半部分见(总结篇二) |